キャラクターに向かっていく弾(自機狙い弾)
今回制作したものはこんな感じになります。
クリックした位置に赤点が移動し、青点から赤点へ黒点を飛ばします。
黒点はクリックした位置(赤点)まで行くと消えます。
お急ぎの方は、まとめへどうぞ。
Math.atan2
JavaScriptには標準組み込みオブジェクトにMathというものがあります。
そのなかのMath.atan2(y, x)という関数があり、端的に言えば、2点間の角度をラジアン単位で返すものです。
気になる人はこちら→※MDN
他にもMath.cos(rad)やMath.sin(rad)などもあります。
ソースコード
class Canvas {
constructor() {
// キャンバスの生成
this.canvas = document.createElement('canvas');
// htmlのbodyに追加
document.body.append(this.canvas);
this.ctx = this.canvas.getContext('2d');
// キャンバスのサイズをブラウザのウィンドウいっぱいにする
this.canvas.width = document.documentElement.clientWidth;
this.canvas.height = document.documentElement.clientHeight;
}
// 画面の塗りつぶしメソッド
canvasFill() {
// 色薄い緑に
this.ctx.fillStyle = 'rgb(191, 255, 191)';
// キャンバスのサイズで塗りつぶす
this.ctx.fillRect(0, 0, this.canvas.width, this.canvas.height);
}
getCanvas() {
return this.canvas;
}
getContext() {
return this.ctx;
}
}// 読み込みが完了したときの処理
window.onload = function() {
init();
};
// 初期処理
const init = function() {
// Canvasの生成
const CanvasClass = new Canvas();
// Canvasの塗りつぶし
CanvasClass.canvasFill();
// 黒点の配列
let blackDots = [];
// Canvasがクリックされた時のイベントを登録する
CanvasClass.getCanvas().addEventListener('click', e => {
// 変数 e には、クリックイベントが格納されている
// 赤点をクリックされた位置に移動する
redDot.x = e.x;
redDot.y = e.y;
// 黒点の生成
const dot = Object.create(blackDot);
// 黒点の位置を青点にする
dot.x = blueDot.x;
dot.y = blueDot.y;
// 黒点の最終地点をクリックされた点にする
dot.endPosX = e.x;
dot.endPosY = e.y;
// 青点から赤点への角度を計算する
dot.angle = calcAngle(redDot, blueDot);
blackDots.push(dot);
});
// 100ms毎にキャンバスを塗潰し、各点を描画する
setInterval(function() {
CanvasClass.canvasFill();
drawDot(CanvasClass.getContext(), blackDots);
}, 100);
}
// 青点から赤点への角度を計算する
const calcAngle = function(red, blue) {
return Math.atan2(red.y - blue.y, red.x - blue.x);
}
// 各点の描画
const drawDot = function(ctx, blackDots) {
// 赤点
ctx.beginPath();
ctx.arc(redDot.x, redDot.y, redDot.radius, 0, 360 * Math.PI / 180, false);
ctx.fillStyle = redDot.color;
ctx.fill();
// 青点
// blueDot.moveDot();
ctx.beginPath();
ctx.arc(blueDot.x, blueDot.y, blueDot.radius, 0, 360 * Math.PI / 180, false);
ctx.fillStyle = blueDot.color;
ctx.fill();
// 黒点の描画
for(let i = 0; i < blackDots.length; i ++) {
blackDots[i].moveDot();
ctx.beginPath();
ctx.arc(blackDots[i].x, blackDots[i].y, blackDots[i].radius, 0, 360 * Math.PI / 180, false);
ctx.fillStyle = blackDots[i].color;
ctx.fill();
}
// 黒点が終点位置にいたら配列から削除する
for(let i = 0; i < blackDots.length; i ++) {
if(!blackDots[i].isRemove) continue;
blackDots = blackDots.splice(i, 1);
}
}
// 赤点
const redDot = {
x: 100,
y: 100,
radius: 10,
color: 'rgba(255, 0, 0, 0.8)',
};
// 青点
const blueDot = {
x: 200,
y: 200,
angle: 0,
radius: 10,
color: 'rgba(0, 0, 255, 0.8)',
// 円状に青点を動かす
moveDot: function() {
this.x += Math.cos(this.angle) * this.radius * 2;
this.y += Math.sin(this.angle) * this.radius * 2;
this.angle ++;
if(this.angle >= 360) this.angle = 0;
}
};
// 黒点
const blackDot = {
x: 0,
y: 0,
endPosX: 0,
endPosY: 0,
radius: 3,
speed: 5,
angle: 0,
color: 'rgba(0, 0, 0, 1)',
isRemove: false,
// 黒点の移動
moveDot: function() {
this.x += this.speed * Math.cos(this.angle);
this.y += this.speed * Math.sin(this.angle);
this.isEndPos();
},
// 黒点が終点位置にいるかチェックする
isEndPos: function() {
let isEndX = false;
if(0 <= this.speed * Math.cos(this.angle)) {
if(this.endPosX <= Math.round(this.x)) isEndX = true;
} else {
if(Math.round(this.x) < this.endPosX) isEndX = true;
}
let isEndY = false;
if(0 <= this.speed * Math.sin(this.angle)) {
if(this.endPosY <= Math.round(this.y)) isEndY = true;
} else {
if(Math.round(this.y) < this.endPosY) isEndY = true;
}
if(isEndX && isEndY) this.isRemove = true;
},
}
自機狙いとは
自機狙いとは、結局のところ点1から点2へ向かって飛んでいく弾です。
今回ならば、青点(点1)から赤点(点2)へと向かっていけば、自機狙いになります。
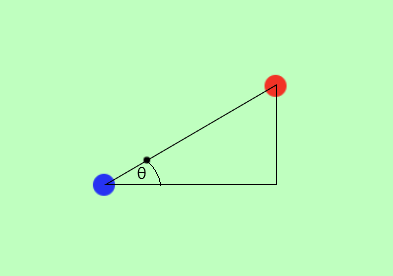
青点から角度θ(シータ)方向へ弾を飛ばせば良いことになります。
2点間の角度
では、角度θを求めるにはどうすればよいのかというと、Mathオブジェクトに便利な関数があります。
ソースコードでは、41行目でその処理をしています。
Math.atan2は座標から角度を求めることができる関数です。
公式では、原点から赤点への角度を求めています。
今回は原点ではなく、青点から赤点への角度を求めるため、赤点の座標 - 青点の座標 とすることで、青点を原点(0, 0)へと移動する処理をしています。
最終的に弾を飛ばしたい座標 - 弾を発射する座標 をし、Math.atan2(y, x)をすることで、2点間の角度が求まるということです。
座標と角度
さて、Math.atan2(y, x)を用いて、青点から赤点への角度が求まりました。
次に赤点へと弾を飛ばす処理についてです。
ソースコードでは、109,110行目になります。
角度が求まっているので、x座標は speed * Math.cos(angle)、y座標は speed * Math.sin(angle) を加算していけば良いことになります。
理由を知っておくと便利なことがあるので、少しだけ紐解いてみます。
cos = cosine(コサイン), sin = sine(サイン), tan = tangent(タンジェント),というものがあります。
高校数学で習う三角関数というやつですね。
さらに、下図の直角三角形ABCにおいて、
BC / AC = sinθ, AB / AC = cosθ, BC / AB = tanθ となります。
少し変形して、 BC = sinθ * AC, AB = cosθ * AC です。
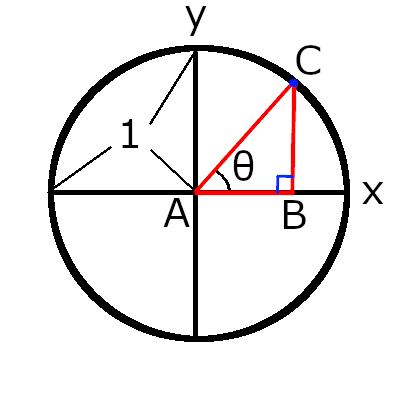
Aは原点(0, 0)であり、同時に半径1の円の中心です。
また、三角形ABCは角CABがθ(シータ)の直角三角形です。
この時の座標Cを考えてみます。
円の半径が1なのでAC = 1ということになります。
ですので、先ほどの三角関数の式はBC = sinθ, AB = cosθ となります。
図の通り、Cのx座標はABの長さ、Cのy座標はBCの長さとなります。
つまり、ABの長さは、AB = cosθ,
また、BCの長さは、 BC = sinθです。
よって、Cの座標は(cosθ, sinθ)となります。
さて、今回は原点A(0, 0)から半径1の距離にある点Cの座標を求めました。
では、半径2の距離にある点C'はどうなるかというと、先ほど述べたように、x座標はABの長さでy座標はBCの長さです。
つまり、BC = sinθ * AC, AB = cosθ * AC なので、BC = sinθ * 2, AC = cosθ * 2 となります。
同様に半径3の距離にある点C''、半径4の距離にある点C'''、…としていくと、A点から角度θ方向に向かって伸びる直線の軌跡が出来上がります。
この軌跡が、発射点から任意の角度方向の点へと向かっていく弾道となるわけです。
まとめ
2点間の角度 = Math.atan2(到達地点.y - 発射地点.y, 到達地点.x - 発射地点.y)
飛ばす弾の座標.x = 現在の弾のx座標 + Math.cos(2点間の角度) * 弾の速さ
飛ばす弾の座標.y = 現在の弾のy座標 + Math.sin(2点間の角度) * 弾の速さ
これだけです。
